写在前面
在安全领域,伪随机数是很常见的,接下来我来简单唠唠伪随机数。以下内容是在经过在网上查找学习后的简略总结。
伪随机数之初学习
1、定义
伪随机数:
伪随机数是用确定性的算法计算出来自[0,1]均匀分布的随机数序列。并不真正的随机,但具有类似于随机数的统计特征,如均匀性、独立性等。在计算伪随机数时,若使用的初值(种子)不变,那么伪随机数的数序也不变。伪随机数可以用计算机大量生成,在模拟研究中为了提高模拟效率,一般采用伪随机数代替真正的随机数。模拟中使用的一般是循环周期极长并能通过随机数检验的伪随机数,以保证计算结果的随机性。
说到伪随机数,就需要提一下真随机数和准随机数。
真随机数:
- 真随机数数列是不可预计的,因此也不可能重复产生两个相同的真随机数数列。
- 真随机数只能用某些
随机物理过程来产生。 - 如果采用随机物理过程来产生真随机数,理论上不存在什么问题。但在实际应用时,要做出速度很快,而又准确的随机数物理过程产生器是非常困难的。
准随机数:
准确随机数概念是来自如下的事实:要实现严格数学意义上的随机数,在理论上虽然可行,但在实际中却是不可行的,也米有这个必要。关键是要保证“随机”数数列具有能产出所需要的结果的必要特性。
2、生成方法
一般地,伪随机数的生成方法主要有以下3种:
(1) 直接法(Direct Method),根据分布函数的物理意义生成。缺点是仅适用于某些具有特殊分布的随机数,如二项式分布、泊松分布。
(2) 逆转法(Inversion Method),假设U服从[0,1]区间上的均匀分布,令X=F-1(U),则X的累计分布函数(CDF)为F。该方法原理简单、编程方便、适用性广。
(3)接受拒绝法(Acceptance-Rejection Method):假设希望生成的随机数的概率密度函数(PDF)为f,则首先找到一个PDF为g的随机数发生器与常数c,使得f(x)≤cg(x),然后根据接收拒绝算法求解。由于算法平均运算c次才能得到一个希望生成的随机数,因此c的取值必须尽可能小。显然,该算法的缺点是较难确定g与c。
伪随机数生成器(PRNG)一般采用逆转法,其基础是均匀分布,均匀分布PRNG的优劣决定了整个随机数体系的优劣[7]。下文研究均匀分布的PRNG。
总结:
- 1.计算机的伪随机数是由随机种子根据一定的计算方法计算出来的数值。所以,只要计算方法一定,随机种子一定,那么产生的随机数就是固定的。
- 2.只要用户或第三方不设置随机种子,那么在默认情况下随机种子来自系统时钟。
3、随机种子
随机种子,一种以随机数作为对象的以真随机数(种子)为初始条件的随机数。一般计算机的随机数都是伪随机数,以一个真随机数(种子)作为初始条件,然后用一定的算法不停迭代产生随机数。
接下来我们用程序深入理解一下
import numpy as np
num = 0
while (num < 5):
np.random.seed(0) # 每次循环随机种子不变
print(np.random.rand(1,5)) # 得到一个范围从0到1的 1行5列的随机数
num += 1
print('-------------------------')运行结果:
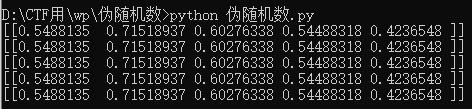
由结果可以看出来,这些都是伪随机数,也就是一直不变的随机数,所以我们可以通过输入随机种子,得到一个初始固定的随机数。随机种子的初始值,是一直不变的。
我们把随机种子的赋值,放到循环外面,意思是只初始化一次。
import numpy as np
num = 0
np.random.seed(0) # 随机种子只初始化一次
while (num < 5):
print(np.random.rand(1,5))
num += 1
print('-------------------------')看到,结果就不一样了,但是初始化第一行的结果还是一样的,这说明初始值一样 ,而且你会发现,无论你运行多少遍,有了随机种子,运行的结果都是一样的
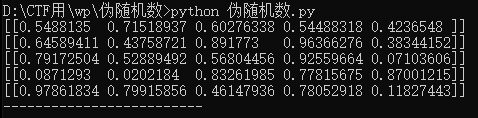
当随机种子没有初始化时,即我们把他注释掉,如果不设置这个值,则系统根据时间来自己选择这个值,此时每次生成的随机数因时间差异而不同。
import numpy as np
num = 0
#np.random.seed(0)
while (num < 5):
print(np.random.rand(1,5))
num += 1
print('-------------------------')第一次结果:
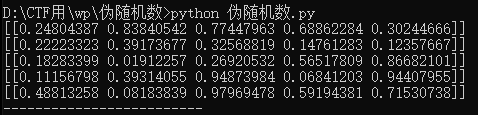
第二次结果:
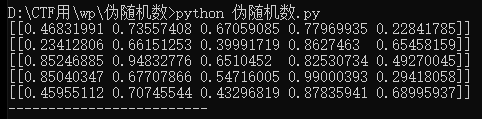
第三次结果:
此时结果就是完全随机的。
总结:
通过随机种子,通过一些复杂的数学算法,你可以得到一组有规律的随机数,而随机种子就是这个随机数的初始值。随机种子相同,得到的随机数一定也相同。
4、伪随机数在web中
就拿BugkuCTF靶场WEB第二题计算器来举个栗子。
可以知道,当式子被点击时,式子底色,数字和数字颜色都随机变化了,也发现不了什么规律。用view-source查看源码,打开"js/code.js"文件。
$(function() {
var code = 9999;
function codes(){
var ranColor = '#' + ('00000' + (Math.random() * 0x1000000 << 0).toString(16)).slice(-6); //随机生成颜色
// alert(ranColor)
var ranColor2 = '#' + ('00000' + (Math.random() * 0x1000000 << 0).toString(16)).slice(-6);
var num1 = Math.floor(Math.random() * 100);
var num2 = Math.floor(Math.random() * 100);
code = num1 + num2;
$("#code").html(num1 + "+" + num2 + "=?");
if ($("#code").hasClass("nocode")) {
$("#code").removeClass("nocode");
$("#code").addClass("code");
}
$("#code").css('background',ranColor);
$("#code").css('color',ranColor2);
}
codes()
$("#code").on('click',codes)
$("#check").click(function(){
if ($(".input").val() == code && code != 9999) {
alert("flag{CTF-bugku-0032}");
} else {
alert("输入有误!");
}
});
}); 顺便发现了flag竟然藏在这里。以前都没有注意到过。
codes()函数中,ranColor,ranColor2,num1,num2这四个变量均是通过一定的计算方法产生的伪随机数。
写在后面:
目前接触到关于随机数的ctf题目较少,以后会根据题目来总结。